Teorema de la media o valor medio para integrales

Teorema del valor medio del cálculo integral

      El teorema del valor medio del cálculo integral dice así:

     Si una función es continua en un intervalo cerrado [a,b], entonces existe al menos un punto c, dentro de ese intervalo que cumple lo siguiente:

¿Qué quiere decir esto? Vamos a verlo

     Si tenemos una función definida en un intervalo [a,b], el área limitada por la función y los rectas x=a y x=b es la siguiente:

     Pues bien, existe un punto c, entre los puntos a y b, donde la función en ese punto tiene un valor de f(c):

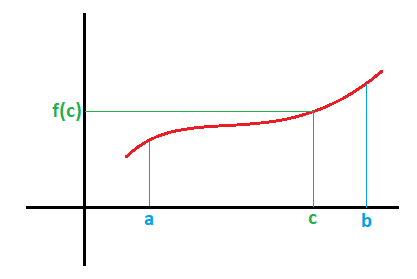
     Se puede formar un rectángulo cuya base es la longitud del intervalo [a,b], es decir, b-a y la altura es la longitud correspondiente al valor de la función en el punto c, es decir f(c)

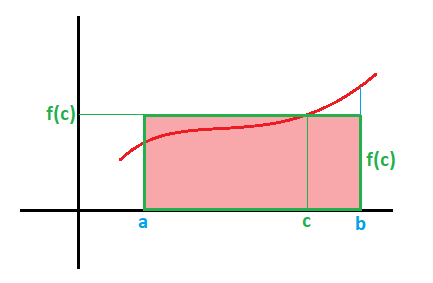
     El área de este rectángulo es igual al área encerrada por la función y los puntos de abcisa a y b, por lo que:

     Donde (b-a).f(c) corresponde al área del triángulo y f(c) corresponde al valor medio de la función f(x) en ese intervalo (o también lo puedes encontrar como altura media) y el punto c es el punto donde se alcanza dicho valor.

     Para poder ver Ejemplos respecto a este tema, se presentan en el enlace a continuación:
"PULSA AQUÍ"