Aplicación de las Integrales en la vida cotidiana
Como todas las ciencias, la matemática posee su implementación en la vida cotidiana, acción que se realiza sin tener una percepción completa de esta, por ello se procede a presentar ciertos ejercicios que demuestran o explican usos de las Integrales en el día a día.
1. Por ejemplo se puede utilizar para calcular la distancia de un lugar a otro, mediante el siguiente ejercicio.

Ejercicios Resueltos
1.Vamos a ver cómo aplicar la fórmula del teorema del valor medio del cálculo integral con un ejercicio resuelto paso a paso.
Es el siguiente: Hallar el valor medio en el intervalo [1,4] y obtener el valor del punto para el cual se verifica dicho valor, de la siguiente función:
La función es continua en el intervalo [1,4], por lo que se puede aplicar el teorema del valor medio del cálculo integral:
Aplicamos la fórmula y nos queda:
Tenemos que calcular el valor medio, es decir, vamos calcular el valor de f(c). Para ello, en primer lugar vamos a calcular la integral definida de la función entre 1 y 4 que tenemos en el primer miembro. Integramos y aplicamos la regla de Barrow:



Cuyo resultado es 69 unidades cuadradas.
Sustituimos la integral del primer miembro por el valor que acabamos de calcular:
Operamos y despejamos f(c), que es el valor medio que nos están pidiendo:
Una vez hemos obtenido cuánto vale el valor medio, vamos a calcular el punto c, para el cual f(c) toma ese valor. Obtenemos f(c), a partir de f(x), sustituyendo la x por la c y nos queda:
Sustituimos ahora f(c) por el valor que acabamos de calcular:
Nos ha quedado una ecuación de segundo grado. Pasamos todos los términos al primer miembro e igualamos a cero:
Resolvemos la ecuación y las soluciones que nos quedan son:

Desechamos la solución negativa al queda fuera del intervalo [1,4] y nos quedamos con la solución positiva. Por tanto, el punto c para el cual la función toma el valor medio es:
3. Ejercicio resuelto aplicando las propiedades de las integrales definidas
Ejercicio 3.1
Calcula el área limitada entre la siguiente función y el eje x:
El área limitada por esta función y el eje x será el área que quede entre la función y los puntos de corte con el eje x, que a su vez serán los límites de integración.
Por tanto, lo primero que tenemos que hacer es calcular los puntos de corte de la función con el eje x.
La función corta con el eje x cuando es igual a cero, por lo que debemos igualar a cero la función y resolver la ecuación de segundo grado que resulta:
Cuyas soluciones son:

Por tanto, la función corta al eje x en los puntos x=-1 y x=2.
Si representamos la función nos queda:
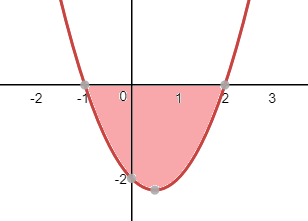
El área que tenemos que calcular queda por debajo del eje x, por lo que será igual a la integral de la función entre -1 y 2, y precedida por un signo menos:
Para eliminar el signo menos, le damos la vuelta a los límites de integración:
Ahora aplicamos la regla de Barrow.
Integramos la función y la dejamos entre corchetes con sus límites de integración:

Realizamos al resta de las funciones primitivas correspondientes sustituyendo la x por -1 y por 2 respectivamente::

Operamos, dejando el segundo paréntesis, ya que tiene delante un signo menos y no equivocarnos en los signos:

Y ahora sí, eliminamos el segundo paréntesis, cambiando de signo los términos que tiene dentro:

Finalmente, reducimos a común denominador y operamos hasta llegar al resultado final:

El área limitada entre la función y el eje x tiene un valor de 9/2 unidades cuadradas.
Ejercicio 3.2
Calcular el área limitada entre la siguiente función y el eje x:
Al igual que en el caso anterior, el área limitada por esta función y el eje x será el área que quede entre la función y los puntos de corte con el eje x.
Por tanto, vamos a calcular los puntos de corte de la función con el eje x.
La función corta con el eje x cuando es igual a cero, por lo que debemos igualar a cero la función y resolver la ecuación que nos queda:
En este caso nos queda una ecuación bicuadrada, que tiene 4 soluciones que son:

Por lo tanto, la función corta al eje x cuatro veces en los puntos -2, -1, 1 y 2, lo que quiere decir también que la función pasa de ser positiva a negativa y viceversa más de una vez.
Si la representamos nos queda de la siguiente manera:

El área de que tenemos que calcular está separada en 3 recintos, por lo que el área total será la suma de los 3 recientos:
El área limitada por la función y los puntos de corte -2 y -1 queda por debajo del eje x. Por tanto, será igual a menos la integral de la función entre -2 y -1, ya que la integral tiene un valor negativo:
Entre los puntos de corte -1 y 1, la función es positiva y el área a calcular queda por encima del eje x, por lo que se calcular como la integral de la función entre -1 y 1:
Por último, entre los puntos de corte x=1 y x=2, la función vuelve a ser negativa, por lo que el área queda por debajo del eje x. El área será igual a menos la integral de la función entre 1 y 2:
Vamos a ir resolviendo cada una de estas áreas.
Empezamos por S1:
Para que el valor de la integral sea positivo, en primer lugar le cambiamos el signo a la integral y e intercambiamos los límites de integración:
Integramos, dejando la primitiva entre corchetes con los límites:

Y aplicamos la regla de Barrow, realizando la resta del valor de la primitiva para x=-2 menos el valor de la primitiva para x=-1:

Y operamos hasta llegar al valor del área de S1:


S1 tiene una área de 22/15 unidades cudadradas.
Seguimos con S2:
Integramos:

Aplicamos la regla de Barrow

Y operamos:


S2 tiene un área de 76/15 unidades cuadradas.
Por último, calculamos el área de S3:
Volvemos la integral positiva intercambiando los límites de integración:
Integramos:

Aplicamos la regla de Barrow

Y operamos:


El área de S3 es 22/15 unidades cuadradas.
Calculamos el área total que es la suma de las áreas de cada reciento:

Por tanto, el área limitada entre la función y el eje x tiene un valor de 8 unidades cuadradas.
Si te das cuenta, S1 y S3 tiene el mismo valor, ya que la función es simétrica. Por tanto, no es necesario volver a calcular S3. Se puede justificar su valor diciendo que es simétrica a S1.
Ejercicio 3.3
Calcular el área limitada entre la siguiente función y el eje x y las rectas x=-4 y x=7:
Para entender mejor el área que nos piden en este ejercicio, representamos tanto la gráfica como las rectas:

El área que queda encerrada entre las rectas y la función, por encima del eje x es el área que nos están pidiendo, es decir, S1 y S2:
Vamos a calcular cada una de las áreas.
En primer lugar, calculamos los puntos de corte de la función con el eje x. Para ello igualamos la función a cero:
Y resolvemos la ecuación de segundo grado resultante:


Las soluciones son x=-3 y x=5:

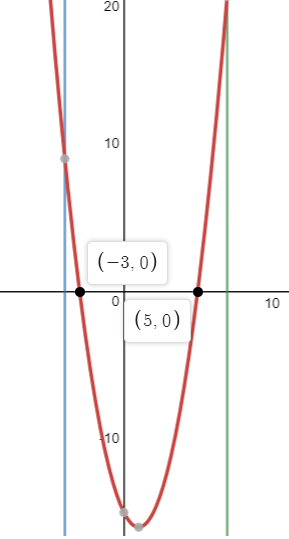
El área S1 la calculamos como la integral de la función entre los límites de integración x=-4 (corte de la recta y la función) y x=-3 (corte de la función y el eje x):
Integramos:

Aplicamos la regla de Barrow

Y operamos:

Para calcular S2 hacemos lo mismo: la calculamos como la integral de la función entre los límites de integración x=5 (corte de la función y el eje x) y x=7 (corte de la recta y la función):


El área encerrada entre la función, las dos rectas y el eje x es la suma de S1 y S2:
Enlaces de Interés
Para visualizar ejercicios respecto al tema hacer click aquí:




No hay comentarios.:
Publicar un comentario