Función Integral

     Sea  una función continua en el intervalo .

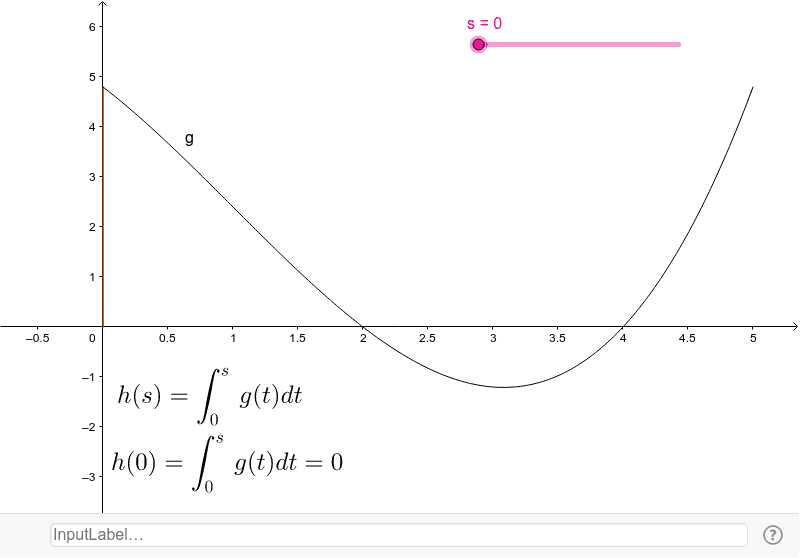
     A partir de esta función se define la función integral:

que depende del límite superior de integración.

     Para evitar confusiones cuando se hace referencia a la variable de , se la llama , pero si la referencia es a la variable de , se la llama .

     Geométrica mente la función integral, , representa el área del recinto limitado por la

curva , el eje de abscisas y las rectas  y .

     A la función integral, , también se le llama función de áreas de  en el intervalo .

Gráficas

Gráfica #1